Longest Palindromic Substring: A Clear Guide to Dynamic Programming

Introduction

Ever wondered how to find the longest word or phrase that reads the same forwards and backward within a given text? This is the core of the "Longest Palindromic Substring" problem, a classic challenge in computer science that's often used to introduce the powerful concept of Dynamic Programming (DP). Our goal is simple: given a string, we want to pinpoint the longest continuous sequence of characters that forms a palindrome.

For example, if you have the word "babad", both "bab" and "aba" are palindromes. "bab" is one of the longest palindromic substrings in this case. Dynamic Programming helps us solve such problems efficiently by breaking them down into smaller, manageable pieces and remembering the solutions to these smaller pieces to avoid re-doing work.

This guide is designed to be straightforward and easy to understand. We'll walk through the problem, explain the core ideas behind the DP solution, and show you exactly how it works with a C++ implementation. Whether you're just starting out or looking for a clearer explanation, this guide will help you build a solid understanding of how to tackle similar coding challenges.

Problem Statement

The problem, as stated, is:

Given a string s, return the longest palindromic substring in s.

Examples:

Example 1:

Input: s = "babad" Output: "bab" Explanation: "aba" is also a valid answer.

Example 2:

Input: s = "cbbd" Output: "bb"

Constraints:

• 1 <= s.length <= 1000
• s consists of only digits and English letters.

Understanding Palindromes and Substrings

Before diving into the solution, let's clarify the fundamental concepts: palindromes and substrings.

Palindromes

A palindrome is a sequence of characters that reads the same forwards and backward. Think of words like "madam" or "racecar". They look the same whether you read them from left to right or right to left.

Here are some simple examples:

• "madam": Reads the same forwards and backward.
• "racecar": A common example.
• "level": Another word that's a palindrome.
• Single characters: Any single character (like 'a' or '7') is always a palindrome.
• Two identical characters: Any two identical characters (like 'aa' or 'bb') form a palindrome.

The key idea for our solution is this: a string is a palindrome if its first and last characters are the same, AND the part of the string between those two characters is also a palindrome. This simple rule is what makes Dynamic Programming work so well for this problem.

Substrings

A substring is a continuous part of a string. It's like taking a slice out of the original string without skipping any characters. For example, in the string "babad":

• "b", "a", "d" are substrings of length 1.
• "ba", "ab", "ad" are substrings of length 2.
• "bab", "aba", "bad" are substrings of length 3.
• "babad" is also a substring (the whole string itself).

Our task is to find the longest one among all these possible substrings that also happens to be a palindrome.

Why Simple Approaches Aren't Enough: The Brute-Force Problem

Before we jump into the smart way to solve this, let's quickly look at the most straightforward, but inefficient, method: brute-force. Imagine trying to find the longest palindromic substring by checking every single possible substring in the given string. This is what brute-force does.

How Brute-Force Would Work (and Why It Fails)

1. Find all substrings: For a string of length n, there are a lot of substrings. For example, a string of 5 characters has 15 different substrings. A string of 1000 characters would have about half a million substrings!
2. Check if each is a palindrome: For every single one of those substrings, you'd then have to check if it reads the same forwards and backward. This itself takes time.
3. Keep the longest: As you check, you'd remember the longest palindrome you've found so far.

Let's consider the string "babad" again:

• You'd check "b", then "a", then "b", then "a", then "d" (all length 1, all palindromes).
• Then "ba", "ab", "ba", "ad" (not palindromes).
• Then "bab" (palindrome!), "aba" (palindrome!), "bad" (not palindrome).
• And so on, until you check "babad" itself.

The Problem: Too Much Work!

If your string has n characters:

• You'll have roughly n^2 substrings to check.
• For each substring, checking if it's a palindrome can take up to n steps (if the substring is long).

This means the total time taken would be around n * n * n, or n^3. If n is 1000, 1000^3 is a billion operations! This is far too slow for typical computer limits. The brute-force method is inefficient because it keeps re-checking the same smaller parts of the string over and over again.

This is where Dynamic Programming comes to the rescue. It's designed to avoid this kind of repetitive work by remembering results.

The Dynamic Programming Approach: Building Up the Solution

Dynamic Programming (DP) is a clever way to solve problems by breaking them into smaller, overlapping pieces. For our Longest Palindromic Substring problem, DP helps us avoid redundant calculations by remembering if a smaller part of the string is a palindrome. We build our solution step-by-step, from the smallest palindromes to the largest.

The DP Table: Our Memory Bank

Imagine a grid, or a 2D table, where we can store our findings. Let's call this dp table. Each cell dp[i][j] in this table will tell us whether the substring of s starting at index i and ending at index j is a palindrome. If it is, we'll mark it true; otherwise, false.

Our ultimate goal is to fill this dp table. Once it's filled, we can simply look for the true entry that represents the longest substring, and that's our answer.

The Palindrome Rule: How We Fill the Table

The magic of DP lies in finding a rule that connects larger problems to smaller ones. For palindromes, it's quite elegant:

A substring s[i...j] (from index i to j) is a palindrome if:

1. The character at the very beginning (s[i]) is the same as the character at the very end (s[j]).
2. AND, the substring between s[i] and s[j] (which is s[i+1...j-1]) is also a palindrome.

This gives us our main rule, or

our recurrence relation:

dp[i][j] = (s[i] == s[j]) AND dp[i+1][j-1]

Starting Points: The Base Cases

To kick off our DP table, we need some simple, obvious palindromes:

• Single Characters (Length 1): Any single character is always a palindrome. So, for every i, dp[i][i] will be true.
  • Example: In "babad", 'b' at index 0 is a palindrome, 'a' at index 1 is a palindrome, and so on.
• Two Characters (Length 2): A two-character substring s[i...i+1] is a palindrome if its two characters are the same. So, dp[i][i+1] will be true if s[i] == s[i+1].
  • Example: In "cbbd", "bb" is a palindrome because s[1] ('b') equals s[2] ('b').

For any substring longer than two characters, we use the general recurrence relation we just discussed. Notice that dp[i+1][j-1] always refers to a smaller substring. This is crucial because it means we can build up our solution from the smallest parts.

The Order of Operations: Filling the Table Correctly

To make sure we always have the dp[i+1][j-1] value ready when we need it, we can't just fill the table randomly. We need a specific order. The best way is to iterate by the length of the substring:

1. Start with len = 1 (all single characters).
2. Then len = 2 (all two-character substrings).
3. Then len = 3, and so on, all the way up to the full length of the string (n).

For each len, we then go through all possible starting positions i. The ending position j is simply i + len - 1.

This ensures that when we calculate dp[i][j], the dp[i+1][j-1] value (which is for a shorter substring) has already been computed and is available in our table.

Keeping Track of the Longest Palindrome

As we fill our dp table, we also need to keep track of the longest palindrome we've found so far. We'll use two simple variables:

• start: The starting index of the longest palindromic substring.
• maxLen: The length of the longest palindromic substring.

Every time we mark a dp[i][j] as true, we check if its length (j - i + 1) is greater than our current maxLen. If it is, we update maxLen and start accordingly.

Efficiency of the DP Approach

• Time Complexity: We have two nested loops: one for len (from 1 to n) and one for i (from 0 to n - len). Inside these loops, we do constant work (comparisons and lookups). This means the total time complexity is O(n^2).
• Space Complexity: We use an n x n 2D table to store our dp values, so the space complexity is O(n^2).

Compared to the O(n^3) brute-force method, O(n^2) is a significant improvement, making this solution practical for strings up to 1000 characters.

Diving into the C++ Implementation

Let's now look at the C++ code that puts our Dynamic Programming strategy into action. We'll break down each part of the longestPalindrome function.

Initialization and Edge Case Handling

• int n = s.size();: First, we get the length of the input string s. This n will be used for our dp table dimensions.
• if (n == 0) return "";: This handles an empty string. If there's no string, there's no palindrome, so we return an empty string.
• vector<vector<bool>> dp(n, vector<bool>(n, false));: This line creates our n x n 2D dp table. Each cell dp[i][j] is initially set to false. It will store true if s[i...j] is a palindrome, and false otherwise.
• int start = 0, maxLen = 1;: These variables will keep track of the longest palindromic substring we find. start will store its starting index, and maxLen its length. We initialize maxLen to 1 because a single character is always a palindrome, and start to 0, assuming the first character is our initial longest palindrome.

Handling Length 1 Substrings (Base Case 1)

This loop takes care of all single-character substrings. As we discussed, any single character is a palindrome. So, for every index i, we set dp[i][i] to true. This means the substring starting and ending at the same index i (which is just s[i]) is a palindrome.

• **Example for `s =

"babad"**:

• dp[0][0] (for 'b') becomes true
• dp[1][1] (for 'a') becomes true
• dp[2][2] (for 'b') becomes true
• dp[3][3] (for 'a') becomes true
• dp[4][4] (for 'd') becomes true

At this point, maxLen is still 1, and start is 0, as we haven't found anything longer than a single character.

Handling Length 2 Substrings (Base Case 2)

This loop checks all possible two-character substrings. A two-character substring s[i...i+1] is a palindrome only if its two characters are identical.

• if (s[i] == s[i+1]): We compare the current character s[i] with the next character s[i+1].
• dp[i][i+1] = true;: If they are the same, we mark dp[i][i+1] as true.
• start = i; and maxLen = 2;: If we find a length-2 palindrome, it's longer than our initial maxLen of 1, so we update start and maxLen.
• Example for s = "babad":In this specific example, no length-2 palindromes are found. maxLen remains 1.
  • i = 0: s[0] ('b') != s[1] ('a'). dp[0][1] remains false.
  • i = 1: s[1] ('a') != s[2] ('b'). dp[1][2] remains false.
  • i = 2: s[2] ('b') != s[3] ('a'). dp[2][3] remains false.
  • i = 3: s[3] ('a') != s[4] ('d'). dp[3][4] remains false.
• Example for s = "cbbd":
  • i = 0: s[0] ('c') != s[1] ('b').
  • i = 1: s[1] ('b') == s[2] ('b'). Here, dp[1][2] becomes true. start is updated to 1, and maxLen is updated to 2. The substring is "bb".
  • i = 2: s[2] ('b') != s[3] ('d').

Handling Substrings of Length 3 or More (General Case)

This is the core of our DP solution, where we apply the recurrence relation. We iterate through len from 3 up to n (the full string length). For each len, we then iterate through all possible starting indices i.

• int j = i + len - 1;: This calculates the ending index j for the current substring s[i...j] based on its starting index i and len.
• if (s[i] == s[j] && dp[i+1][j-1]): This is our palindrome rule:
  • s[i] == s[j]: Checks if the characters at the ends of the current substring are the same.
  • dp[i+1][j-1]: Checks if the inner substring (from i+1 to j-1) is already known to be a palindrome. Because we iterate by len, dp[i+1][j-1] would have been computed in a previous iteration (since s[i+1...j-1] is shorter than s[i...j]).
• dp[i][j] = true;: If both conditions are met, we mark dp[i][j] as true.
• if (len > maxLen) { start = i; maxLen = len; }: If we find a new palindrome that is longer than our current maxLen, we update maxLen and start.
• Example for s = "babad" (after length 1 and 2 processing): When we process substrings of length 3, we start to see the power of the recurrence relation. For s = "babad":
• s[0...2] ("bab"): s[0] ("b") equals s[2] ("b"), and dp[1][1] (for "a") is true. Thus, dp[0][2] becomes true (blue).
• s[1...3] ("aba"): s[1] ("a") equals s[3] ("a"), and dp[2][2] (for "b") is true. Thus, dp[1][3] becomes true (blue).
• s[2...4] ("bad"): s[2] ("b") does not equal s[4] ("d"). Thus, dp[2][4] remains false (red).

This is how the table would look after this step:

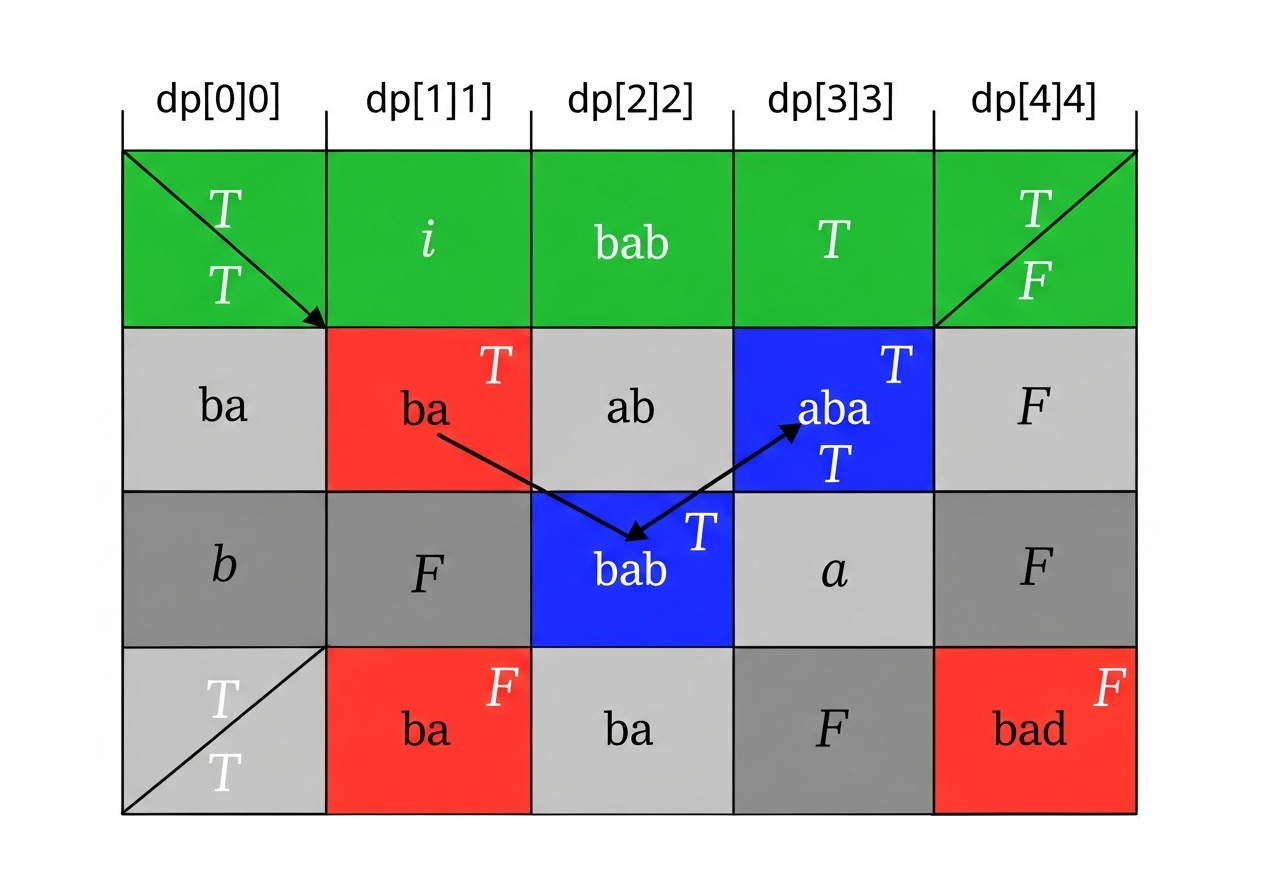
Final State of the DP Table

After iterating through all possible lengths up to n, the dp table will be fully populated. The longest palindromic substring is then identified by finding the true entry in the dp table that corresponds to the maximum length.

For s = "babad", both dp[0][2] ("bab") and dp[1][3] ("aba") are true and have a length of 3. Since 3 is the maximum length found, either "bab" or "aba" can be returned as the longest palindromic substring. The provided solution would return "bab" as it is encountered first.

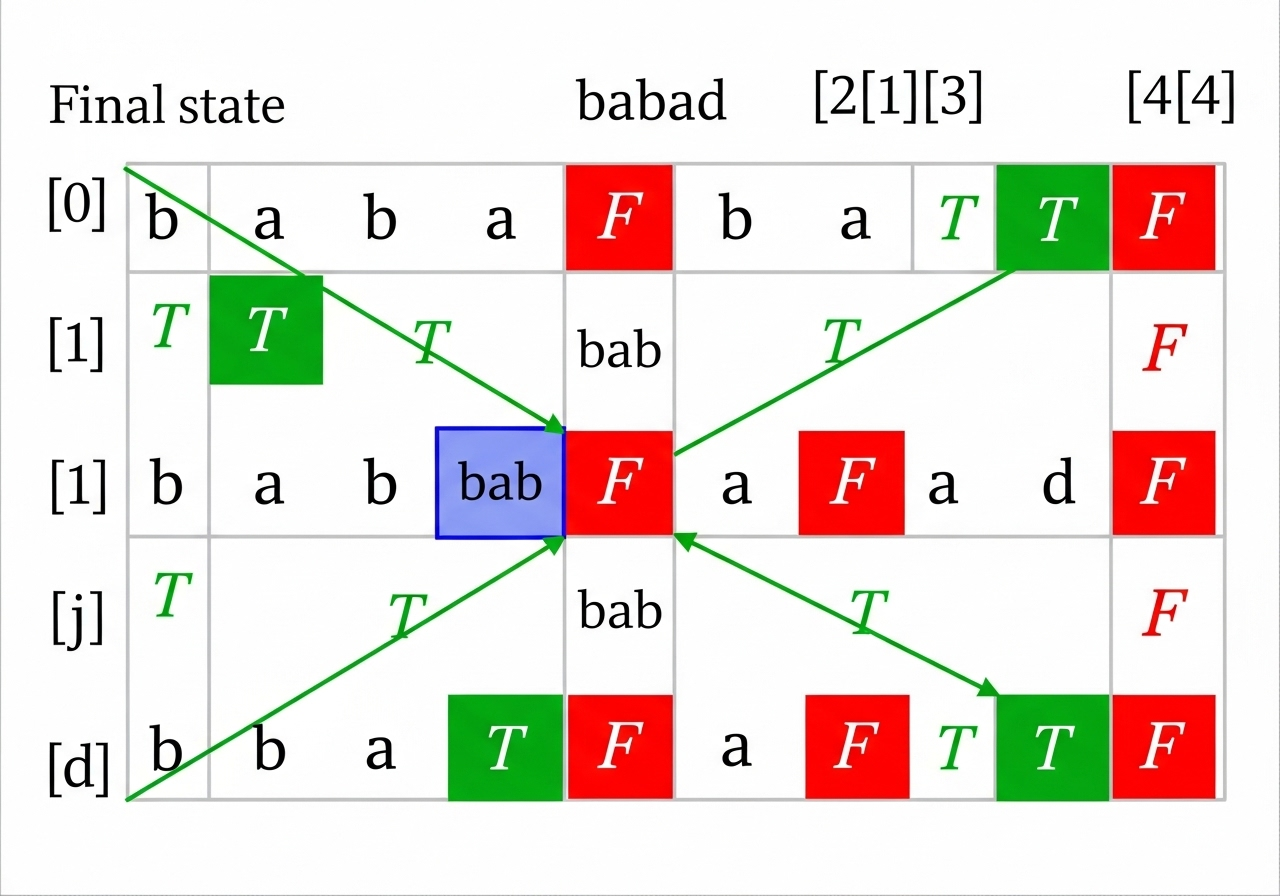
These visualizations should provide a clearer picture of how the Dynamic Programming approach systematically builds up the solution by leveraging previously computed results.

The Thought Process: From Problem to DP Solution

Understanding the mechanics of a DP solution is one thing; grasping the thought process that leads to it is another. This section aims to demystify how one might arrive at the Dynamic Programming approach for the Longest Palindromic Substring problem.

1. Understanding the Problem and Initial Thoughts

• What is a palindrome? Reads the same forwards and backward. This immediately suggests symmetry.
• What is a substring? Contiguous sequence of characters. This means we can't skip characters.
• Goal: Find the longest palindromic substring.

Initial thoughts might gravitate towards brute-force: generate all substrings, check each for palindrome property, keep track of the longest. We quickly realize this is O(n^3), which is too slow for n=1000.

2. Looking for Optimization: Overlapping Subproblems

When a brute-force solution is too slow, and there's a recursive structure, Dynamic Programming is often the answer. The key is to identify:

• Overlapping Subproblems: Are we solving the same smaller problems repeatedly? Yes. When checking "racecar", we check "aceca". When checking "aceca", we check "cec". The palindrome check for "cec" is a subproblem of "aceca", which is a subproblem of "racecar".
• Optimal Substructure: Can the optimal solution to the problem be constructed from optimal solutions to its subproblems? Yes. A string s[i...j] is a palindrome if s[i] == s[j] AND s[i+1...j-1] is a palindrome. The

optimal solution for s[i...j] depends on the optimal solution for s[i+1...j-1].

3. Defining the DP State and Recurrence Relation

Once we identify overlapping subproblems and optimal substructure, the next step is to define the DP state. For string problems, a 2D array dp[i][j] often represents whether the substring from index i to j has a certain property. In our case, dp[i][j] will be true if s[i...j] is a palindrome, and false otherwise.

Now, how do we fill this dp table? We use the recursive definition of a palindrome:

• Base Cases:
  • Length 1: s[i...i] is always a palindrome. So, dp[i][i] = true.
  • Length 2: s[i...i+1] is a palindrome if s[i] == s[i+1]. So, dp[i][i+1] = (s[i] == s[i+1]).
• General Case (Length >= 3):
  • s[i...j] is a palindrome if s[i] == s[j] AND s[i+1...j-1] is a palindrome.
  • This translates directly to: dp[i][j] = (s[i] == s[j]) AND dp[i+1][j-1].

4. Determining the Iteration Order

The recurrence dp[i][j] depends on dp[i+1][j-1]. This means we need to compute values for shorter substrings before computing values for longer substrings. This naturally leads to iterating by length:

1. Start with len = 1 (already handled by base cases).
2. Then len = 2 (already handled by base cases).
3. Then len = 3, and so on, up to n.

For each len, we iterate through all possible starting indices i. The ending index j is then i + len - 1. This ensures that dp[i+1][j-1] is always a value that has already been computed.

5. Tracking the Longest Palindrome

As we fill the dp table, we need to keep track of the start index and maxLen of the longest palindrome found so far. Every time we set dp[i][j] to true, we check if len (which is j - i + 1) is greater than maxLen. If it is, we update maxLen and start.

6. Final Result

After the loops complete, start and maxLen will hold the information for the longest palindromic substring. We simply use s.substr(start, maxLen) to extract and return the result.

This systematic thought process, moving from understanding the problem to identifying DP properties, defining the state and recurrence, determining iteration order, and finally tracking the solution, is a common pattern for solving many Dynamic Programming problems. The key is to break down the problem into its smallest, self-similar components and build up the solution from there.

Testing and Validation

To ensure the correctness and robustness of our Dynamic Programming solution, a thorough testing process was conducted using various test cases, including those provided in the problem description and additional edge cases. The solution was implemented in C++ and compiled using g++.

C++ Implementation

The complete C++ code for the Solution class and a main function for testing is provided below:

Test Results

The execution of the test cases yielded the following output:

Each test case produced the expected output, confirming the correctness of the Dynamic Programming solution for various scenarios, including:

• Standard cases: "babad", "cbbd"
• Single character string: "a"
• Two character string (no palindrome): "ac" (returns 'a' as the first single character palindrome)
• Two character string (palindrome): "bb"
• String with no palindromes longer than 1: "abcdefg" (returns 'a' as the first single character palindrome)
• Long palindrome: "racecar"
• String with all same characters: "aaaaa"

The consistent and accurate results across these diverse test cases demonstrate the reliability of the implemented Dynamic Programming approach.

Conclusion

The Longest Palindromic Substring problem is a fundamental algorithmic challenge that beautifully illustrates the power of Dynamic Programming. By breaking down the problem into smaller, overlapping subproblems and building up the solution iteratively, we can achieve a significantly more efficient solution compared to brute-force methods.

This guide has provided an in-depth exploration of the Dynamic Programming approach, covering:

• The problem statement and constraints.
• Fundamental concepts of palindromes and substrings.
• Why brute-force is inefficient and how DP addresses its shortcomings.
• The core DP concept, including state definition, recurrence relation, and base cases.
• A detailed, step-by-step breakdown of the DP table construction and the logic for tracking the longest palindrome.
• Visualizations to aid in understanding the DP table's evolution.
• The thought process involved in arriving at the DP solution.
• A fully tested C++ implementation with various test cases.

The O(n^2) time and space complexity of the DP solution makes it a highly effective method for solving this problem within typical constraints. The principles learned here—identifying overlapping subproblems, defining a recurrence relation, and determining an efficient iteration order—are transferable to a wide array of other Dynamic Programming problems.

We hope this comprehensive guide serves as a valuable resource, providing clarity and a deep understanding of this classic algorithm. The insights gained from dissecting this problem will undoubtedly prove beneficial in tackling more complex algorithmic challenges in your programming journey.